Kembali lagi bersama saya di blog tetamatika, tetamatika memberikan berbagai administrasi guru, materi ajar, media pembelajaran yang berkaitan dengan pelajaran matematika. Kali ini saya akan membahas tentang materi Fungsi Linear dan Fungsi Kuadrat Kelas X Semester 1.
FUNGSI LINIER
Fungsi adalah hubungan matematis antara suatu variabel dengan variabel lainnya. Unsur-unsurpembentuk fungsi adalah variabel, koefisien, dan konstanta.
Variabel adalah unsur yang sifatnya berubah-ubah dari satu keadaan ke keadaan lainnya. Variabel dapat dibedakan menjadi variabel bebas dan variabel terikat. Variabel bebas :variabel yang menjelaskan variabel lainnya. Adapun Variabel terikat adalah variabel yang diterangkan oleh variabel bebas.
Koefisien adalah bilangan atau angka yang diletakkan tepat di depan suatu variabel, terkait dengan variabel yang bersangkutan.
Konstanta sifatnya tetap dan tidak terkait dengan suatu variabel apapun.
1). Pengertian fungsi linier
Fungsi linier adalah suatu fungsi yang variabelnya berpangkat satu atau suatu fungsi
yang grafiknya merupakan garis lurus. Oleh karena itu fungsi linier sering disebut
dengan persamaan garis lurus (pgl) dengan bentuk umumnya sbb.:
f : x → mx + c atau

Apabila b bernilai positif : Y = 2 + 2X maka kurva bergerak dari kiri bawah ke kanan atas

3). Gradien dan persamaan garis lurus
a). Garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) memiliki gradien m:
m = y1-y2 atau m = y2-y1
x1-x2 x2-x1
b. Persamaan garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) adalah:
y-y1 = x-x1
y2-y1 x2-x1
c. Persamaan garis lurus (pgl) yang bergradien m dan melalui titik A(x1, y1) adalah:
y = m (x – x1 ) + y1
4). Menentukan gradien dari persamaan garis lurus (pgl)
@ Persamaan garis lurus : ax + by = c maka gradiennya m = - a/b
@ Persamaan garis lurus : y = ax + b maka m = a
@ Garis yang sejajar sumbu x memiliki persamaan y = c dan m = 0
@ Garis yang sejajar sumbu y memiliki persamaan x = c dan tidak memiliki gradient
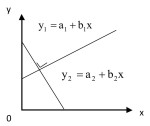
5). Titik potong dua buah garis
Menentukan titik potong dua buah garis lurus identik dengan menyelesaikan
penyelesaian sistem persamaan linier dua variabel baik dengan metode eleminiasi,
metode substitusi maupun metode grafik
6). Hubungan dua buah garis
Dua garis yang bergradien m1 dan m2 dikatakan sejajar jika m1 = m2 dan tegak lurus jika m1 x m2 = -1
Berimpit
Dua garis lurus akan berimpit apabila persamaan garis yang satu merupakan kelipatan dari garis yang lain. Dengan demikian , garis akan berimpit dengan garis
akan berimpit dengan garis  , jika
, jika

Sejajar
Dua garis lurus akan sejajar apabila lereng/gradien garis yang satu sama dengan lereng/gradien dari garis yang lain. Dengan demikian , garis akan sejajar dengan garis
akan sejajar dengan garis 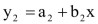 , jika
, jika
Berpotongan
Dua garis lurus akan berpotongan apabila lereng/gradien garis yang satu tidak sama dengan lereng/gradien dari garis yang lain. Dengan demikian , garis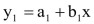 akan berpotongan dengan garis
akan berpotongan dengan garis 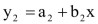 , jika
, jika
Tegak lurus
Dua garis lurus akan saling tegak lurus apabila lereng/gradien garis yang satu merupakan kebalikan dari lereng/gradien dari garis yang lain dengan tanda yang berlawanan. Dengan demikian , garis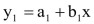 akan tegak lurus dengan garis
akan tegak lurus dengan garis 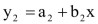 , jika atau
, jika atau
PERSAMAAN KUADRAT
Persamaan kuadrat merupakan bentuk persamaan yang pangkat terbesar variabelnya adalah 2. Bentuk umumnya adalah dengan
dengan  , a, b, dan c adalah koefisien dan x merupakan variabelnya.
, a, b, dan c adalah koefisien dan x merupakan variabelnya.
Contoh: ,
,  , dan sebagainya.
, dan sebagainya.
Menentukan Akar-akar Persamaan Kuadrat
Akar-akar maksudnya adalah nilai yang membuat
yang membuat  hasilnya sama dengan 0. Sebagai contoh, jika
hasilnya sama dengan 0. Sebagai contoh, jika  membuat
membuat  , maka
, maka  disebut sebagai akar-akar dari persamaan kuadrat
disebut sebagai akar-akar dari persamaan kuadrat 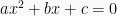 .
.
Untuk menentukan akar-akar, ada tiga metode yang biasa digunakan, yaitu metode pemfaktoran, melengkapkan kuadrat sempurna, dan metode rumus abc. Namun metode melengkapkan kuadrat sempurna jarang atau cukup sulit untuk digunakan dalam menentukan akar-akar, sehingga tidak akan dibahas di pembahasan ini.
 di atas disebut dengan diskriminan (D).
di atas disebut dengan diskriminan (D).
Contoh:
Jenis-jenis Akar Persamaan Kuadrat
Pada contoh-contoh di atas, kita melihat terdapat dua buah akar-akarnya, dan keduanya merupakan bilangan riil. Namun ada kalanya suatu persamaan kuadrat hanya mempunyai satu akar riil (akar-akarnya kembar), atau bahkan tidak mempunyai akar-akar riil.
Naahh, untuk mengetahui apakah suatu persamaan kuadrat mempunyai dua akar riil, satu akar riil (kembar), atau tidak mempunyai akar-akar riil, kita dapat melihat Diskriminan nya (D), yaitu
Jika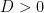 , maka kedua akarnya riil dan berlainan .
, maka kedua akarnya riil dan berlainan .
Jika , maka kedua akar-nya kembar (satu akar riil).
, maka kedua akar-nya kembar (satu akar riil).
Jika , maka kedua akarnya tidak riil (imajiner).
, maka kedua akarnya tidak riil (imajiner).
Contoh:
Jika diketahui bahwa mempunyai satu akar riil, tentukanlah nilai
mempunyai satu akar riil, tentukanlah nilai 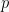 .
.
Jawab:
Karena hanya mempunyai satu akar riil, berarti .
.
Dengan demikian,%5E2+-+4+%5Ccdot+4+%5Ccdot+p+%3D+0&bg=f9f9f9&fg=000000&s=0) .
. .
.
 .
.
f(x) = mx + c atau
y = mx + c
m adalah gradien / kemiringan / kecondongan dan
c adalah konstanta
2). Melukis grafik fungsi linier
Langkah-langkah melukis grafik fungsi linier
a Tentukan titik potong dengan sumbu x, y = 0 diperoleh koordinat A( x1, 0)
b Tentukan titik potong dengan sumbu y, x = 0 diperoleh koordinat B( 0, y1)
c hubungkan dua titik A dan B sehingga terbentuk garis lurus
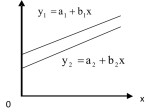
Persamaan linier juga dapat ditulis ditulis dengan simbol y = ax + b (ini untuk memudahkan kita dalam memahami gambar)
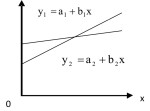
Jika b bernilai positif : fungsi linier digambarkan garis dari kiri bawah ke kanan atas
Jika b bernilai negatif : fungsi linier digambarkan garis dari kiri atas ke kanan bawah
Jika b bernilai nol : digambarkan garis yg sejajar dengan sumbu datar x

Gambar Fungsi Linear
Apabila b bernilai negatif : Y = 10 - 2X maka kurva bergerak dari kiri atas ke kanan bawah
c adalah konstanta
2). Melukis grafik fungsi linier
Langkah-langkah melukis grafik fungsi linier
a Tentukan titik potong dengan sumbu x, y = 0 diperoleh koordinat A( x1, 0)
b Tentukan titik potong dengan sumbu y, x = 0 diperoleh koordinat B( 0, y1)
c hubungkan dua titik A dan B sehingga terbentuk garis lurus
Persamaan linier juga dapat ditulis ditulis dengan simbol y = ax + b (ini untuk memudahkan kita dalam memahami gambar)
Jika b bernilai positif : fungsi linier digambarkan garis dari kiri bawah ke kanan atas
Jika b bernilai negatif : fungsi linier digambarkan garis dari kiri atas ke kanan bawah
Jika b bernilai nol : digambarkan garis yg sejajar dengan sumbu datar x
Gambar Fungsi Linear
Apabila b bernilai negatif : Y = 10 - 2X maka kurva bergerak dari kiri atas ke kanan bawah
Apabila b bernilai positif : Y = 2 + 2X maka kurva bergerak dari kiri bawah ke kanan atas
3). Gradien dan persamaan garis lurus
a). Garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) memiliki gradien m:
m = y1-y2 atau m = y2-y1
x1-x2 x2-x1
b. Persamaan garis lurus yang melalui titik A(x1, y1) dan B(x2, y2) adalah:
y-y1 = x-x1
y2-y1 x2-x1
c. Persamaan garis lurus (pgl) yang bergradien m dan melalui titik A(x1, y1) adalah:
y = m (x – x1 ) + y1
4). Menentukan gradien dari persamaan garis lurus (pgl)
@ Persamaan garis lurus : ax + by = c maka gradiennya m = - a/b
@ Persamaan garis lurus : y = ax + b maka m = a
@ Garis yang sejajar sumbu x memiliki persamaan y = c dan m = 0
@ Garis yang sejajar sumbu y memiliki persamaan x = c dan tidak memiliki gradient
5). Titik potong dua buah garis
Menentukan titik potong dua buah garis lurus identik dengan menyelesaikan
penyelesaian sistem persamaan linier dua variabel baik dengan metode eleminiasi,
metode substitusi maupun metode grafik
6). Hubungan dua buah garis
Dua garis yang bergradien m1 dan m2 dikatakan sejajar jika m1 = m2 dan tegak lurus jika m1 x m2 = -1
Berimpit
Dua garis lurus akan berimpit apabila persamaan garis yang satu merupakan kelipatan dari garis yang lain. Dengan demikian , garis
 akan berimpit dengan garis
akan berimpit dengan garis  , jika
, jika

Sejajar
Dua garis lurus akan sejajar apabila lereng/gradien garis yang satu sama dengan lereng/gradien dari garis yang lain. Dengan demikian , garis
 akan sejajar dengan garis
akan sejajar dengan garis 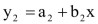 , jika
, jika

Berpotongan
Dua garis lurus akan berpotongan apabila lereng/gradien garis yang satu tidak sama dengan lereng/gradien dari garis yang lain. Dengan demikian , garis
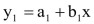 akan berpotongan dengan garis
akan berpotongan dengan garis 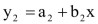 , jika
, jika

Tegak lurus
Dua garis lurus akan saling tegak lurus apabila lereng/gradien garis yang satu merupakan kebalikan dari lereng/gradien dari garis yang lain dengan tanda yang berlawanan. Dengan demikian , garis
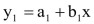 akan tegak lurus dengan garis
akan tegak lurus dengan garis 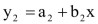 , jika atau
, jika atau

PERSAMAAN KUADRAT
Persamaan kuadrat merupakan bentuk persamaan yang pangkat terbesar variabelnya adalah 2. Bentuk umumnya adalah
Contoh:
Menentukan Akar-akar Persamaan Kuadrat
Akar-akar maksudnya adalah nilai
Untuk menentukan akar-akar, ada tiga metode yang biasa digunakan, yaitu metode pemfaktoran, melengkapkan kuadrat sempurna, dan metode rumus abc. Namun metode melengkapkan kuadrat sempurna jarang atau cukup sulit untuk digunakan dalam menentukan akar-akar, sehingga tidak akan dibahas di pembahasan ini.
Metode Pemfaktoran
Persamaan kuadrat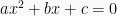 diubah menjadi
diubah menjadi (x-x_2)%3D0&bg=f9f9f9&fg=000000&s=0) , sehingga akar-akarnya adalah
, sehingga akar-akarnya adalah 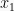 dan
dan 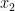 .
.
Misalkan kita ingin memfaktorkan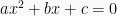 .
.
Cara memfaktorkannya adalah:
Pertama, carilah dua bilangan, misalnya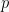 dan
dan  , sehingga jika dijumlahkan, hasilnya adalah
, sehingga jika dijumlahkan, hasilnya adalah  , sedangkan jika dikalikan, hasilnya adalah
, sedangkan jika dikalikan, hasilnya adalah  . Dengan kata lain,
. Dengan kata lain,  dan
dan  .
.
Jika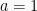 , maka bentuk pemfaktorannya adalah
, maka bentuk pemfaktorannya adalah (x%2Bq)%3D0&bg=f9f9f9&fg=000000&s=0) , sehingga akar-akarnya adalah
, sehingga akar-akarnya adalah  atau
atau  .
.
Jika , maka bentuk pemfaktorannya adalah
, maka bentuk pemfaktorannya adalah (x+%2B+%5Cfrac%7Bq%7D%7Ba%7D&bg=f9f9f9&fg=000000&s=0) , sehingga akar-akarnya adalah
, sehingga akar-akarnya adalah  atau
atau  .
.
Contoh:
Tentukanlah akar-akar dari persamaan kuadrat (a)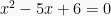 dan (b)
dan (b)  .
.
Jawab:
(a):
 dan
dan  . Cari dua bilangan,
. Cari dua bilangan, 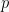 dan
dan  , sehingga
, sehingga  dan
dan  .
.
Kedua bilangan tersebut adalah dan
dan  , karena
, karena +%3D+-5&bg=f9f9f9&fg=000000&s=0) dan
dan  .
.
Maka pemfaktorannya adalah)(x+%2B+(-2))+%3D+0&bg=f9f9f9&fg=000000&s=0) atau
atau (x-2)%3D0&bg=f9f9f9&fg=000000&s=0) ,
,
Persamaan kuadrat
Misalkan kita ingin memfaktorkan
Cara memfaktorkannya adalah:
Pertama, carilah dua bilangan, misalnya
Jika
Jika
Contoh:
Tentukanlah akar-akar dari persamaan kuadrat (a)
Jawab:
(a):
Kedua bilangan tersebut adalah
Maka pemfaktorannya adalah
sehingga akar-akarnya adalah  atau
atau  .
.
(b):
Sama dengan (a), cari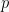 dan
dan  sehingga
sehingga  dan
dan  .
.
Maka didapat dan
dan  .
.
Maka pemfaktorannya adalah(x+%2B+%5Cfrac%7B9%7D%7B6%7D&bg=f9f9f9&fg=000000&s=0) , sehingga akar-akarnya adalah
, sehingga akar-akarnya adalah  atau
atau  .
.
Jadi, akar-akar persamaan kuadrat tersebut adalah atau
atau  .
.
(b):
Sama dengan (a), cari
Maka didapat
Maka pemfaktorannya adalah
Jadi, akar-akar persamaan kuadrat tersebut adalah
Metode Rumus ABC
Tidak semua bentuk persamaan kuadrat dapat difaktorkan. Sebagai contoh, kita tidak dapat memfaktorkan bentuk di mana tidak ada bilangan bulat
di mana tidak ada bilangan bulat 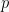 dan
dan  yang memenuhi
yang memenuhi  dan
dan  .
.
Hal ini karena akar-akar persamaan tersebut bukanlah berbentuk bilangan bulat atau bilangan rasional, tetapi bilangan irasional.
Untuk menentukan akar-akarnya, kita dapat menggunakan rumus abc berikut:
 .
.
Jadi, akar-akarnya adalah dan
dan 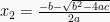 .
.
Tidak semua bentuk persamaan kuadrat dapat difaktorkan. Sebagai contoh, kita tidak dapat memfaktorkan bentuk
Hal ini karena akar-akar persamaan tersebut bukanlah berbentuk bilangan bulat atau bilangan rasional, tetapi bilangan irasional.
Untuk menentukan akar-akarnya, kita dapat menggunakan rumus abc berikut:
Jadi, akar-akarnya adalah
Contoh:
Tentukanlah akar-akar dari  .
.
Jawab:
 , dan
, dan  , sehinga dengan menerapkannya pada rumus abc di atas, kita dapat:
, sehinga dengan menerapkannya pada rumus abc di atas, kita dapat:+%5Cpm+%5Csqrt%7B(-3)%5E2+-+4+%5Ccdot+1+%5Ccdot+1%7D%7D%7B2+%5Ccdot+1%7D&bg=f9f9f9&fg=000000&s=0) .
.
 .
.
Berarti akar-akarnya adalah dan
dan 
Jawab:
Berarti akar-akarnya adalah
Jenis-jenis Akar Persamaan Kuadrat
Pada contoh-contoh di atas, kita melihat terdapat dua buah akar-akarnya, dan keduanya merupakan bilangan riil. Namun ada kalanya suatu persamaan kuadrat hanya mempunyai satu akar riil (akar-akarnya kembar), atau bahkan tidak mempunyai akar-akar riil.
Naahh, untuk mengetahui apakah suatu persamaan kuadrat mempunyai dua akar riil, satu akar riil (kembar), atau tidak mempunyai akar-akar riil, kita dapat melihat Diskriminan nya (D), yaitu
Jika
Jika
Jika
Contoh:
Jika diketahui bahwa
Jawab:
Karena hanya mempunyai satu akar riil, berarti
Dengan demikian,
Jadi, nilai 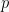 yang memenuhi adalah
yang memenuhi adalah  .
.
Jumlah dan Hasil Kali Akar-akar
Jika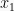 dan
dan 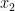 merupakan akar-akar persamaan kuadrat
merupakan akar-akar persamaan kuadrat  , maka berlaku hubungan:
, maka berlaku hubungan:
 .
.
 .
.
Contoh:
Jika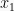 dan
dan 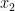 merupakan akar-akar dari
merupakan akar-akar dari  , tentukanlah nilai dari
, tentukanlah nilai dari  .
.
Jawab:
Persamaan kuadrat di atas tidak bisa difaktorkan, jadi akar-akarnya berbentuk bilangan irasional, yang mana menjadi sulit bagi kita untuk menghitung nilai .
.
Namun, kita tidak perlu menghitung satu-satu berapa nilai dari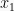 dan
dan 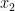 , tapi bisa menghitung langsung nilai dari
, tapi bisa menghitung langsung nilai dari  , dengan menggunakan rumus jumlah dan hasil kali akar-akar.
, dengan menggunakan rumus jumlah dan hasil kali akar-akar.
Perhatikan bahwa%5E2+-+2x_1+x_2&bg=f9f9f9&fg=000000&s=0) .
.
Dari rumus di atas kita dapat: dan
dan 
Dengan demikian,%5E2+-+2+%5Ccdot+%5Cfrac%7B10%7D%7B3%7D&bg=f9f9f9&fg=000000&s=0) .
. .
.
Menyusun Persamaan Kuadrat Baru
Kita dapat menyusun sebuah persamaan kuadrat baru dari informasi akar-akarnya. Jika akar-akarnya adalah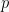 dan
dan  , maka persamaan kuadrat barunya adalah:
, maka persamaan kuadrat barunya adalah:
x+%2B+pq+%3D+0&bg=f9f9f9&fg=000000&s=0) .
.
Contoh:
Contoh: Persamaan kuadrat yang akar-akarnya 3 dan 5 adalahx+%2B+3+%5Ccdot+5+%3D+0&bg=f9f9f9&fg=000000&s=0) .
.
Jika
Contoh:
Jika
Jawab:
Persamaan kuadrat di atas tidak bisa difaktorkan, jadi akar-akarnya berbentuk bilangan irasional, yang mana menjadi sulit bagi kita untuk menghitung nilai
Namun, kita tidak perlu menghitung satu-satu berapa nilai dari
Perhatikan bahwa
Dari rumus di atas kita dapat:
Dengan demikian,
Menyusun Persamaan Kuadrat Baru
Kita dapat menyusun sebuah persamaan kuadrat baru dari informasi akar-akarnya. Jika akar-akarnya adalah
Contoh:
Contoh: Persamaan kuadrat yang akar-akarnya 3 dan 5 adalah
FUNGSI KUADRAT
Fungsi kuadrat merupakan suatu fungsi yang pangkat terbesar variabelnya adalah 2. Mirip dengan persamaan kuadrat, namun berbentuk suatu fungsi.
Bentuk umumnya adalah:
Contoh:
Dengan demikian,
Grafik/Kurva Fungsi Kuadrat
Jika digambarkan pada koordinat Cartesius, grafik fungsi kuadrat berbentuk parabola. Parabola nya terbuka ke atas jika
Berikut ini langkah-langkah dalam menggambarkan grafik/kurva nya:
Pertama, tentukan titik potong
Kemudian, tentukan titik potong terhadap sumbu
Setelah itu, tentukan sumbu simetri nya. Sumbu simetri merupakan garis yang membagi dua parabola menjadi sama besar. Titik potong sumbu simetri terhadap sumbu
Terakhir, tentukan titik puncak (titik balik maksimum atau minimum) grafiknya. Titik puncak merupakan titik di mana nilai
Koordinat titik puncak parabola adalah:
Di mana D adalah diskriminan, yaitu
Setelah mendapatkan titik-titik di atas, maka kita dapat menggambar grafik fungsi kuadrat dengan menghubungkan titik-titik diatas dengan garis yang berbentuk parabola.
Agar parabolanya terlihat lebih halus (smooth), kita dapat menghitung/menentukan titik-titik lain yang dilewati oleh kurva/fungsi
Berikut ini merupakan contoh grafik fungsi kuadrat

Contoh Soal:
Jika
Jawab:
Nilai minimum tersebut merupakan titik puncak
Dengan demikian, dengan menggunakan rumus titik puncak kita dapat:
Titik puncak =
Dengan demikian,
Hubungan Diskriminan Grafik Fungsi Kuadrat
Jika pada persamaan kuadrat nilai diskriminan dapat kita gunakan untuk mengetahui apakah akar-akarnya riil, kembar, atau tidak mempunyai akar-akar riil, pada fungsi kuadrat kita dapat menggunakan nilai diskriminan untuk mengetahui apakah grafiknya memotong sumbu
Berikut ini sifat-sifatnya:
Jika
Jika
Jika
Jika
Kembali ke Bahan Ajar Mata Pelajaran Matematika SMA/SMK/MA Kurikulum 2013 Revisi


0 Komentar untuk "FUNGSI (FUNGSI LINEAR DAN FUNGSI KUADRAT)"